サイコロをふる神
大学の学部生のときに卒論で分子動力学法を用いた計算(だけじゃなくて実験もやったけどね)をして以来、何かとそういう計算に関わることがあったわけだけれど、そう言えば僕はモンテカルロ法というのを仕事に使ったことがない。
モンテカルロ法、というのは、その名から想像される通り、サイコロ→乱数を用いて行う一種のシミュレーションである。モンテカルロ法といっても非常に多岐に渡るわけだけど、僕の関わる分野でこの名が出てくるとき、そのほとんどは統計力学的事象を乱数で解くことを指す。もともとかのフォン・ノイマンが中性子の挙動を計算するのに考案した、という話だから、ある意味一番ファンダメンタルな使い方かもしれない……とか書いても、そんなの分からないよ、と思われる方が大半だと思うので、もう少し分かりやすい話を書くことにする。
まず、この図を見ていただきたい。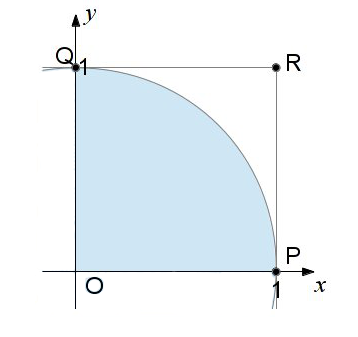
何の変哲もない扇形の図なのだけど、いま、この図中の正方形 OPRQ の中に点を打つことを考える。正方形 OPRQ の中に入るように点を打つと、それは扇形 OPQ の中になるときと、外になるときがある。いま、十分に数多く、てんでバラバラになるように点を打ったとして、全体の点の数を N、扇形 OPQ の中に打たれた点の数を n とすると、点の数は打たれる点の範囲の面積に比例するので、
N : n = (1 × 1) : (1 × 1 × π ÷ 4)となるはずである。これを π に関する式として整理すると、
π = 4 n / Nとなる。
いやだから何なんだ、と思われるかもしれないが、要するに、一様乱数 x, y(ただし x, y = [0,1])で定められる点 (x, y) を十分大きな数である N 個打ったとき、
x2 + y2 ≦ 1を満たすものの数を n 個とすると、N と n から円周率を求めることができるのである。
これは数学的には何をやっていることになるのか、というと、円の面積を積分で求め、そこから円周率を算出する、という操作である。円の場合はこんなことをする必要はないわけだけど、解析的に積分するのが難しいような関数であっても、この方法で積分することができるわけで、これをモンテカルロ積分という。積分区間で乱数で点を打ち、それが積分される領域に属するかどうか検定することで、面積や体積を求めることができるわけだ。
しかし、完全に一様、かつバラバラな乱数というものがあるのかどうか、ということが問題になるわけだ。たとえば、僕等が使うプログラミング言語…… C とか Fortran とか、最近だったら Java とか C# とか……には大抵「乱数を生成する関数」というのがある。もっと卑近な例で言うなら Excel にだってあるわけだが、これを使ってこのような計算をして、果たして円周率が計算できるのか、というと、実はできない。これは計算機の能力の問題ではなくて、計算機で「良質な」乱数を得ることが難しい、ということを反映している。
現在使われている乱数生成法で最も良質、かつ高速なものとされているMersenne Twisterを用いてこの計算を行ってみると、N = 109 の場合で、3.1416112599999999 という計算結果を得た。なんと、10億個も乱数のペアを計算して、せいぜい4、5桁の精度でしか円周率が計算できない、ということになるわけだ。
……とか書くと、あたかも Mersenne Twister に問題があるみたいに思われそうだけど、そもそもこうやって計算を行った場合の「分解能」を考えると、これはおおむね N の平方根と同じ桁数ということになるから、4〜5桁、ということで、上の結果はちゃんとこの分解能の範囲内で妥当な結果を出せている。
もちろん、僕はこのような計算を、円周率を求めるためにしているわけではない。そもそもこの円の求積法による計算は乱数を使う必要などない。等間隔に細かく、規則的に点を打ったって計算はできる(し、その方が桁数の制限の中ではより妥当な結果を返すだろう)のだが、こういう計算で既知の値に対してどのような計算結果が得られるか、で、乱数の質を判定することができるわけで、その判定のためにこういう計算をすることがある、というわけである。また、Mersenne Twister の名誉のためにもフォローしておくけれど、Mersenne Twister は現存する乱数の中では非常に素性がいいものとされている。素性のいいものを活かすも殺すも、使う側の理解度と使い方にかかっている、というわけなので、どうか誤解されないように。



